Welcome - Editorial
A welcome to the first Compass Points, and a news of what's going on in the surveying world.
Lighting Suuntos - Bob Buecher
First a short piece from Bob Buecher, first published on the Cavers' Forum email discussion list (see later). He details an effective way of lighting your Suunto instruments with surface mounted LEDs.
Survex Release - Wookey/Olly Betts
Next is a discussion of some of the issues facing surveying and surveyors in this country. Some words on how thinking about these started the SURVEX project which addresses some of these issues. Then a summary of SURVEX functionality is given.
Reading List - Wookey
We have a list of articles to complement Dave Irwin's list of required reading for those interested in surveying on computers.
What is Least Squares, and why use it? - Olly Betts.
The least squares system of error distribution is used by many survey programs. Olly Betts endeavours to remove the mystique about it and explain why it is the most appropriate way to deal with data containing the sort of random errors associated with normal survey data. There are those who think that loop closure in any form is not a good idea, because it merely hides errors in the data. They have a point, but dealing with gross errors is a separate issue from dealing with the normal errors generated by the survey process. Systems to deal best with this (gross error) problem remain a subject for further work.
Calibration Data Analysis - Wookey
By way of some non-computing matter, an analysis of calibration data, gained on 4 years of CUCC Austria expeditions is included. It arguably raises more questions than it answers.
Many of the reading references are in Compass & Tape, the journal of the Survey and Cartography Section on the NSS (National Speleological Society), the American national caving body. They have been publishing journals and having a big 'best survey' competition at their national conference for years. Many of the subjects of interest to us all have been discussed in C&T, and I may be reprinting some of their articles here. The BCRA library should have a complete set of these, but for those who wish to join personally, membership is very cheap, and so are back issues.
Membership (including a years quarterly issues), is $4.00, back issues are $1.00 each plus $1.00 postage per order. Payment must be in US$, and cheques drawn on a U.S. bank. (payable to 'SACS'). Send monies and back issue requests to the Treasurer, Bob Hoke, 6304 Kaybro St. Laurel, MD 20707 (Tel 301-725-5877).
Send all correspondence and submissions to:-
The Editor, Compass Points, 28 Spalding Way, Cambridge, CB1 4NR. Tel 0223 243215 (H), 0223 811679 (W),
or E-Mail to Wookey@Aleph1.co.uk.
Articles can be on paper, but the preferred format
is ASCII text files with paragraph breaks, but if they are particularly
technical (i.e. lots of sums) then Microsoft Word documents are
probably best, WordPerfect docs are also OK. Floppies can be either
size, any DOS format, although RISCOS floppies (or Mac, Atari
or Amiga at a pinch) will also do. Even PCW 3" discs are
feasible - but don't send them the day before the deadline! For
these we can deal with Impression or Mac Word docs, but nothing
much else.
This is the first in what will hopefully be an illustrious series. The CREG has decided to have a "Surveyors' corner" in the newsletter, and I have been nobbled to 'edit' it. The idea is to provide a forum for discussion of all survey-specific issues, within the CREG framework. This may be a prelude to a new special interest group forming but that requires a lot of work, and volunteers for the task are few and far between.
I hope that all those with an interest in surveying will subscribe to this publication and that everyone will have something to say, and will say it. As Dave Gibson said in the CREG Journal Number 12, 'Surveyors are an argumentative bunch of people'. If he's right this should make interesting reading. The exact direction of Compass Points will be determined by its readership, and what you write for it. So get scribbling.
This first issue has gone to all CREG members, as well as a few other people who we think might be interested. You will be invited to indicate if you do/don't/only want to receive Compass Points from then on.
The advantages of remaining within CREG are the existing organisation, and the regular journal. The disadvantages are the obscurity (to other surveyors who might be interested, it not being obvious that the CREG covers surveying too) and the current strong bias towards the computing side of surveying, as opposed to the presentation and data-gathering aspects, although there is no reason why this shouldn't change.
As mentioned by Pete Cousins in CREG Newsletter 12, the Earth's magnetic field is somewhat variable over time, and to properly reference compass data to the Map grid, accurate temporal magnetic deviation information is required. In the US a number of magnetic models are accessible by modem link, and by choosing a model and specifying the time, date, place & altitude, you can get fairly accurate values for the magnetic dip & azimuth. Does such a service exist in the UK, or Europe?
The cavers' forum is an Email-based discussion group. It is based around a 'mail-reflector' which means that everyone sends their submissions to a central point which 'reflects' them all back out to the members. Anyone can join by sending a request to cavers-request@vlsi.bu.edu.
You just need a modem, some communication software and a computer to access the forum, which has approximately the equivalent of a couple of sides of A4 discussion a day. This will only cost you a few pence (if any), depending how you access the net. The nature of the medium means that it is extremely up-to date, so for example, rescue reports/analysis often appear the day after a rescue. It currently has a predominantly American membership, but there are quite a few British, and some from France, Australia, Russia, Ukraine, Austria, New Zealand and more.
Give it a try if you can.
Future articles in the pipeline:
Survey Draughting using !Draw - The pros and cons of using standard PC vector graphics packages to produce the final printed version of a survey.
Survey Data Exchange/Description Meta-Language. On-going efforts to define a standard.
In the longer term there will be a comparative review of every survey program I can lay my hands on, using the same datasets, probably including: SMAPS 5.2, SURVEX, SURVEYOR 88, CAVEMAP, SURVEY, KARST, CML and COMPASS (in no particular order).
Suunto use, improvement, and refurbishment.
Bob Buecher
It is fairly easy to put a small LED on the top of the compass. Several years ago Speleonics (#6, Fall 1986) published an article by Richard Market on installing an LED. He recommended making an "L" shaped bracket to hold the LED on the top of the Suunto over the compass dial. The short end of the "L" bracket went behind the lanyard eyebolt and held it in place.
I used a similar system on one of my suuntos for several years but drilled a small hole at the edge of the aluminium above the compass dial, the wire was routed through the interior of the compass and came out near the lanyard eyebolt. Then through the inside of a p-cord lanyard to a 9-volt battery.
The LED leads had to be filed very short to prevent the steel from interfering with the compass. I originally made the mistake of trying to mount the LED inside the Suunto in a position similar to the factory light.
This turned out to be a very poor location for the LED which gave only weak light on the dial. After drilling a few more holes I switched to the top mounting as described by Market.
When I sent my Suunto in to have the hairline replaced I ended up with a completely new Suunto! Perhaps they thought all of the holes I had drilled were the problem. So I set about constructing a new LED light for my Suunto.
What I now have is a surface mount LED, these are about 3mm long and 2mm wide and fit nicely into a 1/8" hole. I built a holder out of a piece of circuit board 1.5" long and 0.25" wide. I filed a grove down the middle to create two conductors in the copper coating. Wires are attached at the opposite end and fed through another small hole in the board for strain relief.
I use the rubber cases which also allows me to tuck the LED boards under the rubber. The wire comes out at the lanyard and the inside a p-cord lanyard to a 9-volt battery. There is no switch as the battery is good for 30 to 50 hours at 5 to 10 ma. The light is very bright and makes reading very easy. The leads on the LED are very small and cause no change in the bearings.
The other day while looking through an electronics catalogue (Newark) I saw some batteries that looked similar to those used in the Suunto internal lights. In fact they are the same battery a National Lithium battery model BR-425. The cost was only $1.98 each instead of the $10 I've seen elsewhere.
Wookey / Olly Betts
As has been mentioned in the CREG journal before by various people there is a need to address some long-term issues in surveying in the UK - especially with reference to the use of computers. Survey data, and stations, get lost over time, usually disappearing with whoever did the original work. There is no central library of survey data, and even if there was, any computer data in it would be almost useless as almost all the data is in different formats. This incompatibility has largely arisen because everyone who has wanted to ease their workload by using a computer has more or less had to write their own survey program to do it. This of course has meant massive duplication of effort around the country, and indeed the world.
Recognising these issues back in 1989 Olly Betts & I decided to do our bit to address the last couple. So we initiated the SURVEX (Survey Excellence) project. We felt that the two issues of multiple survey programs and multiple data formats were connected, and one way to deal with the data problem was to get everyone using the same survey program.
The only way to do that was to make one that was a) free, and b) better than that which was currently available. Because many cavers only have access to computers through other people, or have old, cheap, machines we felt it very important to cater for the lowest possible machine spec, and for the program to be portable to all computers, with interchangeable data, no matter what machine was used.
Other design considerations were the necessary ability to take in data from almost any source:- other programs, spreadsheets, foreign languages, etc. This meant that the basic input would be ASCII text files with a very general format. We decided not to write a specific data entry editor, as it would be very time-consuming, and impossible to please everyone, but just to let people use their own favourite text editors. A data-entry editor will probably be added later, producing text files in the standard format.
Other requirements were that it was powerful enough to deal with big, complex, systems, but simple to use if you only wanted to do straightforward things.
It also had to be as fast as possible, and extensible so that later developments could be included with minimum difficulty (e.g. passage walls, windowed front-end, etc.).
Another corollary of the philosophy is that all the source code for the program is freely available, so that anyone can change the program to do what they want, or port it to other computers. We hope to involve other interested people in expanding the various aspects of SURVEX, whilst we co-ordinate the development so that the enhancements are spread around to everybody with each new version. The problem with this is that many of those who have an interest have already written their own software, and thus will be more enthused about working on their own project, than one that is seen as "someone else's". Whilst this will possibly increase the overall rate of development, which benefits Joe Surveyor, it isn't efficient, and it still leaves us with multiple data formats.
So don't think of SURVEX as Olly's & mine, think of it as the Cave Radio Group's, or even better the BCRA's. It hasn't been endorsed as such yet, but then we are the only people who can do that in any meaningful way. So, if you think all this is a good idea, get a copy, spread it around, try it and tell us which features you think are good, which are bad - and the new features you would like first.
After 3 years development we now have something that can be used by anyone to process their own data. It's not 'finished' by any means (version 1.0 is still at least a year away). We have made this early release available for people to criticise. It is currently somewhat basic in terms of the user interface (command line/batch file), and some of the facilities that it contains cannot yet be configured without re-compilation (e.g. symbol re-definition). Later releases will have a windowed front end for MS Windows, RISC OS, X-windows etc.
Distinguishing features:
It's free!
Multi-platform (from lowly 8088 PCs to UNIX systems)
Powerful (in terms of survey complexity)
Versatile (in terms of input data)
Fast processing of survey data
Hi-speed mouse and/or keyboard controlled survey viewer
Good printer/plotter support
Source code freely available
Data processing:
Cave complexity limited only by available memory
Versatile system for hierarchical survey station naming
Separate treatment of plumbed legs
Free-text input with user-definable symbols, so you can choose the separator, decimal point, command prefix etc. This aids import from other programs, spreadsheet data, foreign languages etc.
Network reduction by least squares. Standard errors calculated for each leg
Printer support:
Multi-page printouts (for big plots on small printers)
8, 9 and 24 pin dot matrix (Epson, IBM Proprinter, and compatibles)
PCL - i.e. all deskjets, laserjets and compatibles
Postscript
HPGL driver - for various pen plotters
Canon BJ series special driver to come
Graphics:
DOS graphics support for VGA, EGA, CGA, Hercules, 8514a, et al
Acorn RISC OS at various resolutions
X-Windows support
SURVEX can be obtained from:
Wookey: 28 Spalding Way, Cambridge, CB1 4NR 0223 243215(H) 0223 811679(W)
(Olly Betts, 24 Morgans Road, Hertford, HERTS, SG13 8BS, UK. No email address currently - new address in mid-October.)
Please send a formatted disc and a Stamped Self Addressed Envelope
You can also get it from the UK cavers archive site at gserv1.dl.ac.uk by anonymous ftp. It is in the directory /pub/caving/survex. You need the files:
readme.1st - Instructions for installation.
svx025.zip - MSDOS executables.
unzip.exe - Infozip unzip utility.
Pkunzip is OK, but use its -d option.
Also there is src025.zip (or src025.tar.gz) which contains the source code.
Wookey
In a recent CREG Journal Dave Irwin listed a number of articles that should be read by those interested in surveying with computers. There has been a great deal more published on this subject. Here is a list of further articles that I am aware of. It is not exhaustive, but if you read this lot you will be fairly well versed! It is possible that a complete bibliography of cave surveying articles will be produced if there is demand.
Bennet, A-J. 'Application of Computers to Cave Surveying'. Cave Science [14:2] August 1987, pp69-71
Breisch, R.L. 'Cave Visualization Using Voxels - An Alternative to Commercialization'. Compass & Tape [7:4] Spring 1990, pp24-28
Crowl, D.A. 'A Computer Applications System For the Processing of Cave Survey Data'. NSS Bulletin [50-1] June 1988, pp1-8
Fogarty, J 'A Paradigm for Digitized Cave Mapping', Compass & Tape [8:2] Fall 1990, pp3-12
Ganter, J. 'Karst Research and Knowledge: Do We Need Karst Information Systems' 1988 NSS Convention Survey and Cartography Symposium.
Ganter, J. 'CAD For Cave Mapping, A Cautious Assessment'. Compass & Tape [6:4] Spring 1989, pp3-17
Ganter, J. 'Discussion of Wefer's "The Computerization of the Cave Map" and "A North Arrow and Scale for Stage-4 Cave Maps'. C& T [7:4] Spring 1990, pp29-30
Hecker, M 'Micro-based CAD for Cave Map Drafting' 1988 NSS Convention Survey and Cartography Symposium
Kaye, Tom 'Derivation of Cave Closure Weighting Factors', Compass & Tape [9:1&2] Summer, Fall 1991, pp9-11
Kaye, Tom 'Loop Closure Analysis'. CAS Newsletter [3] June 1981, pp262-649
Kelly, Sean & Warren Patrick B. 'The Least Squares Method of Cave Survey Data Reduction based on a Micro Computer', Cave Science[15:1] April 1988, pp29-34
McKenzie, David 'Computer Drawn Passage Walls'. Association for Mexican Cave Studies Newsletter [11], 1980, pp86-89
McKenzie, David. 'Averaging Network Elements', Compass & Tape [4:3&4] Spring 1987, pp43-53
Nepstad, J. 'CAD Application at Wind Cave', Compass & Tape [6:21] Fall 1988, pp3-17
Park, Mel 'Cave Data Language', Compass & Tape [8:1] Summer 1990, p22
Rutherford, J.M & Amundsen, R.M. 'Use of a computer for Cave Survey Data Reduction', NSS Bulletin [36:2] April 1974, pp7-15
Thrun, Robert 'Cave Mapping System Version 4.3', Speleodigest 1976, pp335-340
Waddington, Andy E.R 'Computer Drawn Passage Walls'. Cambridge Underground 1986/76, pp13-14.
Waddington, Andy E.R. 'Random Errors in cave Survey Processing'. Cambridge Underground 1990, pp42-43
Warren, Patrick.B. Distributing Misclosure Errors in Surveying [Easy-to-understand explanation of error distribution]. Cambridge Underground 1986/87, pp19-30
Warren, Patrick B. 'Treatment of Errors in Surveying'. Cambridge Underground 1988, pp16-18
Wefer, Fred.L. 'The Cave Survey Computer Program', Speleodigest 1971, pp307-312
Wefer, Fred.L. 'On the Compass Rule', Speleodigest 1974, pp243-248
Wefer, Fred.L. et. al. 'An Application of Interactive Computer Graphics to the study of Caves', NSS Bulletin [42:2] April 1983, insert
Wefer, Fred.L. 'The Computerization of the Cave Map', Compass & Tape [7:1] Summer 1989, pp3-14
Wefer, Fred.L. 'A North Arrow & Scale for Stage-4 Cave Maps', Compass & Tape [7:2] Fall 1989, pp3-12
Wefer, Fred L. Content Definition and Control for Stage-4 Cave Maps', Compass & Tape [7:4] Spring 1990, pp3-28
Olly Betts Copyright © 1993 Olly Betts.
Published with permission
Cave surveying computer programs commonly use a method called "least squares" to deal with misclosure errors in loops when reducing survey data to produce station positions. Unfortunately, the name suggests that weight is given to the squared error in each reading, so I thought I'd try to explain what is going on. The maths I've used should be easily followed by anyone with O-level or GCSE maths. There may seem to be a lot of equations, but this is because I've tried to be as explicit as possible.
As an example, suppose that we want to estimate the width of a field. To do so, we get n teams of surveyors to measure the distance and call their answers l1, l2, ..., ln. We want some way of turning these n numbers into one number - our estimate of the field's width. If we assume that each measurement is equally reliable, then the "obvious" estimate to take is the average:
So, what about Least Squares?
First of all, here's a result we'll need:
(x-a)2 = (x-a)(x-a) = x(x-a) - a(x-a) = x(x-a) + a(a-x) = x2 - xa + a2 - ax = x2 - 2ax + a2 (*)
Think of x as the field's true width. The error in the first survey team's measurement is l1-x, and the squared error is (l1-x)2 = (x-l1)2. Then the sum of the squared errors in all the measurements, which we'll call S(x), is:
S(x) = (x-l1)2 + (x-l2)2 + ... + (x-ln)2 (1)
The value of x that minimises S (ie m such that S(m) <= S(x) for every x), is called the least square estimate of the width of the field. We can be sure that S(x) has a finite minimum value, since S(x) is the sum of several things squared and something squared is always zero or greater. This means that the lowest value must be zero or greater and hence finite.
Expanding each squared bracket in (1) using (*):
S(x) = (x2
- 2l1x + l12)
+ (x2 - 2l2x
+ l22) + ... + (x2
- 2lnx + ln2)
= x2 + x2
+ ... + x2 [ n brackets
each with an x2 term ]
- 2l1x - 2l2x
- ... - 2lnx [ collecting
terms in x ]
+ l12 + l22
+ ... + ln2 [ collecting
constant terms ]
= nx2 - 2x(l1
+ l2 + ... + ln)
+ (l12 + l22
+ ... + ln2)
To write this more simply, we'll set:
B = (l1 +
l2 + ... + ln)/n
C = (l12 + l22
+ ... + ln2)/n
Note that n, B and C depend only on the readings l1, l2, ..., ln and not on x (the true width).
S(x) = nx2
- 2nBx + nC
= n(x2 - 2Bx + C) [ taking
out a factor of n ]
= n(x2 - 2Bx + {B2
- B2} + C) [ since {B2
- B2} = 0 ]
= n({x2 - 2Bx + B2}
- B2 + C) [ regrouping
the terms ]
= n((x-B)2 - B2
+ C) [ using (*) in reverse ]
Note that anything squared is positive or zero, so
(x-B)2 >= 0
Also, the only number which gives zero when squared is zero, so
(x-B)2 = 0 only if (x-B) = 0 ie x = B
Minimising (x-B)2 minimises S(x) (since the rest of the equation doesn't depend on x), so S(x) is minimised at x=B ie B is the least squares estimate of the width of the field, but B is just the average of the readings, so least squares does what we would have done anyway.
So, big deal. Least squares gives us the average, so why go to all this effort?
(a) It turns out that least squares is easily adaptable to situations where we have interconnected loops. Hence we can find all the station positions in one go, and in no sense can one talk about the order in which the loops are closed.
(b) Another useful thing about least squares is that we can weight the measurements according to how reliable we think they are, by simply dividing each squared error in S(x) by the variance of the measurement. Variance is a statistical term meaning the expected squared error. The definitions of the BCRA grades can be used to do this, so we can process loops with a mixture of survey grades, and more of the misclosure error will get attributed to the lower grade legs.
Wookey
The calibration of compasses, despite having been recognised as very important to any accurate survey years ago, has largely been ignored by many surveyors. I decided to use the Cambridge University Expeditions to Austria over the last few years as an opportunity to do some research on calibration data. The idea was to see exactly what sort of data was obtained with lots of different people, several sets of instruments, and a couple of different calibration points. From this dataset, it should be possible to determine how much reliance can be placed on any one calibration, and the best way to include the data in a survey program.
This article is the first of a pair. It presents the data, and the method, with some discussion of the results. Part two will consist of a proper statistical analysis, and the more direct results of applying the calibrations to the survey data collected at the same time.
Method & Relevant factors
A pair of cairns were set up near the cave entrance about 15m apart, and their tips painted red to distinguish them from surrounding limestone. The procedure was to take a compass reading from the lower to both the upper cairn, and the Braunig Zinken (a top a few kilometers away). Clinometer readings were taken between the cairns both ways. Some people also took compass bearings back from the top to the bottom cairn. The number of readings taken varied from 1 to 5, depending on the enthusiasm of the instrument wielder, the weather, and the lateness of the party! Sightings on the Zinken could only be taken in clear weather.
The magnetic deviation is not included in the plots given here. It about 1 degree (east) and changes very slowly (7 minutes/year) in Austria. As the relative values of the data is all we are interested in, not subtracting between 1deg 5mins (1990), and 1deg 26mins (1993) won't affect my conclusions. - However bear it in mind.
The first year (1990) the cairns were such that a reading between them was taken at an inclination of about 17 degrees. This had the primary effect of giving very variable readings, and showing just how poor compass readings are even in ideal conditions as soon as you get into the region where the compass disc sticks.
In order to get more useful data the top cairn was moved to a lower position for the remaining years. Note that the scale of the compass plot is doubled between 1990 and 1991 because the range is much smaller. It is also possibly relevant to point out that the snow knocked down the cairns each year and the top stone had to be replaced every year so their is a possible position difference of about 10cm at each end between the years. This corresponds to a reading error of up to 0.65 degrees. So although sets of readings within a year should be OK, bear in mind that there may be a small variation to year to year.
The data is grouped by instrument type, and in chronological order. The dates are not shown on these plots, but generally cover a month from the first to the last (approximately the month of July)
The X's mark the mean point for compass readings, and the difference between fore & back sights for the clino. In both cases multiple sights are averaged first and then equal weight given to the fore & back averages when calculating the overall reading. Foresights are filled circles, backsights are empty circles, and Zinken readings are marked with a 'Z'. Note that the zinken readings refer to the bottom scale, whilst cairn readings refer to the top scale.
Conclusions
Unfortunately, my statistical knowledge is minimal so this discussion will be confined to a fairly simple analysis. Part II will discuss the mathematical justification of the somewhat heuristic conclusions which I draw here.
A quick glance at the data firstly shows that there are some pretty hefty variations for people supposedly measuring the same thing! It is difficult to pick out patterns, making it hard to tell whether there is simply not enough data, or if the patterns are obscured by the data presentation. Although the variation for the Zinken points is somewhat less than for the cairn calibration. This is presumably the effect of removing errors related to relatively short legs (parallax, and cairn movement).
The grouping of multiple readings taken by any individual at the same time is very close, even though they may be miles off the overall average. See Julian H 1993 (compass & clino), Pete S 1990, Olly 1990, Wookey 1993 (compass) 1991 (clino). There are only 8 examples (out of 51) where the variation on one calibration is more than 1 degree. You could argue that these were also dependent on the person - eg Tim has two of the three 1990 examples, and Julian T has one in 1990 & one in 1993, but conversely Pete has both a close and widely spaced example in 1993. It seems that an individual tends to give similar readings on different occasions: see Dave F 1990 and Julian T 1991/1993. Again counter-examples exist such as AndyA 1991/1992 who merely demonstrates consistent inconsistency! The high turnover of expedition members means that not enough examples of multiple calibrations over multiple years exist to draw more convincing conclusions.
In a corresponding manner the clino readings are generally closely grouped for any one backsight/foresight set, giving quite convincing averages. Given that magnetic effects can be discounted for clino readings this suggests that either the reading limits or differences in personal optics must account for the variations seen.
It is interesting to note that the variation in readings for the 1990 clino readings is less than for all the other years. Why should a higher clino angle give more consistent readings?
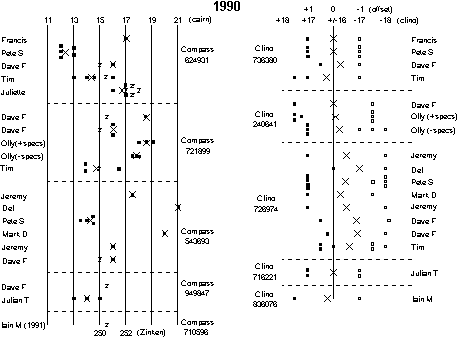
It is fairly clear from the 1990 data that clino 726974 has a zero error of about 0.6 degrees, this is borne out by the later data to some extent, but the offset seems to have reduced to a less significant 0.25 degrees. Apart from this it seems that the variation between instruments is insignificant in comparison to other factors.

The particularly low compass readings in 1993 taken by Adam and Wookey were both taken on the same day - this perhaps gives credence to the idea of occasional large changes in the magnetic field. This could presumably be confirmed from nationally-collected geophysical data. Conversely Dave G's entirely average reading was taken on the same day - hmmm.
Overall the results are fairly woolly, giving no clear indications that the calibration results are sufficiently accurate to be used to adjust the whole of the rest of the survey, however the trends that can be picked out suggest that people are fairly consistent (and the biggest varying factor, with the possible exception of the magnetic field). This suggests that adjusting the data using this information will be better than not doing so.
This hypothesis will be tested in part II.
Despite the apparent inaccuracy and general rubbishness of this data, remember that the variation between the lowest and highest readings is never more than 2.5% for the steep legs, 1.8% for the shallower ones, and 1.3% for the clino readings. Most of the readings lie with 0.8%, which is perhaps all that can be expected.
The obvious follow up to this is to do some more controlled experiments to get a large data set for one day, with several calibration points, several instruments, several people and consistent methods. We tried a small-scale experiment last year around Churchill college, but discovered that the whole place was full of steel and it was impossible to get any meaningful data. Have other people attempted research on this subject?