SMAPS/Lite.
Letters - Bob Thrun on survey software
Survey v2.30 - Steve Neads
Overview of his SURVEY program -the philosophy behind it and the maths to do very large numbers of loop closures.
More-or-less confirmed speakers are: Olly Betts, about the ''Survex' software, Steve Neads, about the 'Survey' software, & Neil Weymouth on 'Searching for caves with Resistivity'. Other speakers are still to be confirmed.
Doug Dotson's address was out-of-date - see below.
I had John Fogarty's name after the description of COMPASS. In fact Larry Fish wrote COMPASS. Fogarty wrote Cave View.
Dear Cave Mapper,
The SMAPS/Lite package is a subset of the SMAPS 5.2 Cave Management System from Speleotechnologies. It was originally devised as a means of running SMAPS in the field on harddiskless notebook and palmtop computers. It became so useful I decided to release it as shareware. This allows a mapper to "test drive" SMAPS before taking the plunge and purchasing it. This is the deal:
SMAPS/Lite and SMAPS run on MSDOS machines.
SMAPS/Lite is copyrighted software and is not being released into the Public Domain. It is being released as shareware.
If you like it and feel that you find it useful, please register it by sending in $25 ($35 outside North America).
When you register, you will receive the complete SMAPS 5.2 users manual and support services via Internet or telephone.
If you decide to purchase SMAPS 5.2, the $25 registration fee will be applied towards the regular purchase price of $99.95 ($109.95 outside North America).
You will also receive a discount on SMAPS/GIS Geographical Information System should you order it by the end of 1993.
Those taking advantage of this offer will receive SMAPS/GIS for $49.95. This includes the software and 50+ page user's manual.
What a great deal!!
SMAPS/Lite includes the hierarchical file system and intelligent survey editors that have been the hallmark of SMAPS for over 10 years. The complete plotting package is also included. All printer drivers are also included for many dot matrix printers and HP laser printers. Sorry, no plotter drivers with this one. Statistical functions including rose diagram trend analysis is included.
What has been removed from SMAPS 5.2 to create SMAPS/Lite is:
GRASS GIS import and export support.
Loop Adjustment
Attributes (color and line styles)
SEF import and export support.
Contour map overlays.
SMAPS/Lite is distributed as 2 ZIP files. smaplite.zip is the complete package with printer drivers for HP laser printers and Epson printers. The remaining drivers (29 Total) are in the file smapdvrs.zip. Hopefully this will allow most people to download the smaller smaplite.zip file and save some time.
SMAPS/Lite is available from Wookey or via Anonymous FTP from the following sites:
vlsi.bu.edu in /pub/cavers-archive/incoming/smaplite.zip
gserv1.dl.ac.uk in /pub/caving/smaplite.zip
Registration and orders should be sent to:
Speleotechnologies
P.O. Box 504
Owings Mills
Maryland 21117-0504
USA
(410) 356-9076
Internet address: dotson@clark.net
I hope that this will provide the opportunity that is intended for a test drive of SMAPS. Any comments and questions are welcome.
Good Cave Mapping -
Doug Dotson, President Speleotechnologies
Survey Software - Bob Thrun
I have several comments on your review of cave survey programs in Compass Points 3.
I would use a finer division in my program classification. My divisions correspond to the history of cave survey program development.
First generation: Summation of successive survey
shots.
Second generation: Sequential loop closure.
Third generation: Simultaneous loop closure.
Fourth generation: Can accept data in any order.
For the first generation, the challenge was to do any kind of processing at all. The programmer worried about handling different input units and how to do branching. There were no loop closures. Nowadays, this kind of program could be written in 5 minutes to an hour, depending on how elaborate the I/O is. Programs of this type are still used for programmable calculators.
The second generation programs featured sequential loop closures. The usual rule was that a loop became fixed after it was once closed. Some of these were developed to handle large surveys. The user worried about the best sequence of inputting and closing loops.
My CMAP program would rate as third generation. It will do simultaneous closures, but it requires that at least one station of a survey shot must have been previously encountered. At the time it was originally written, punched cards were in use, and it was very easy to reverse the order of a deck of cards. Even now, it is not too bad entering the data in reverse order if it is done in small amounts with each survey trip. It is bad if a whole project or expedition is to be handled at once.
Some programs don't fit neatly into the classification. Larry Fish's Compass does sequential closures, but closes the best loops first. It allows a limited number of out-of-sequence survey shots.
It is also possible to classify programs by the graphics, but the graphics do not always follow the overall sophistication of the program. A very sophisticated program might simply write out coordinate data for a drafting program. Conversely, a virtual reality program might utilize a crudely calculated baseline. I can think of examples of each. I do not like to use the term "generation" with respect to graphics because there is no progression by time. I'll use the term "level".
First level: Plots the survey baseline.
Second level: Draws cave walls.
Third level: Models the the cave passage as a solid.
Fourth level: Virtual reality or "Bat Simulator".
I would make no distinction between plots on paper and plots on a computer screen. A program that puts dots alongside each station at the wall distance would rate a 1.5
Another distinction might be made between programs that have their own editor or data entry module and those that read files prepared by general purpose text editors.
SMAPS is not the grandaddy of survey programs. Of just the programs on your list, both CMAP amd Toporobot predate it. SMAPS is probably the most widely used program because it was the first program for the IBM PC that was reasonably complete and ready to use 'off the shelf'. SMAPS was the first program to go commercial, and it was probably the first one where the user interface was designed first.
Besides the programs on your list, there are a great
many that have been used. You see them credited on maps and project
reports, but their authors choose not to distribute them. Often
the programs are unfinished, hard to use, undocumented, or not
general purpose. Many are obsolete and no longer used.
The purpose of this article is to outline the philosophy behind SURVEY v2.30, and to explain the fundamental mathematics by which the program optimizes the loop closures.
SURVEYwas developed to solve the difficult problem of optimizing the spread of the closure errors in a complex cave survey which may have many interconnecting closed traverses and multiple entrances. It was written specifically to solve the author's own problems with the survey of Box Mine in Wiltshire, but is equally suited to complex caves (or indeed simple ones). The first two sections of the Box Mine survey (published in 1990 and 1992) were drawn entirely by hand and the overall 'fit' of the closure errors was done by eye (although a computer program was used to distribute closure errors evenly along individual traverses). The approach taken was to survey a coarse grid covering the whole area of interest and to adjust these loops to fit one another by eye - at this stage there were perhaps 10 loops. These were drawn on the master survey and 'frozen'. All subsequent traverses were then adjusted to fit this framework using the computer program. In some regions the newly added traverses always fitted well, which suggested that the original frame was good, but in other places there was a systematic error indicating a problem with the original frame. The great complexity of the map made finding the bad section impossible, and in any case a complete re-draw was not on! It quickly became clear that the simplistic approach of closing the loops one by one was not sensible for such a complex map and that a more sophisticated method which accounted for all the closure errors simultaneously was required. This led to the following program requirements:
1. Must simultaneously solve a map with many thousands of stations and closed traverses.
2. Must run on a standard PC.
3. Must automatically draw accurate hardcopies (using a suitable plotter) so that the map can be easily replotted as new links are added and the 'fit' is modified.
4. Must allow some points to be fixed (entrances, radio locations etc.).
5. Must allow traverses which appear to be bad to be removed from the optimization (to eliminate distortion of the fit due to gross errors).
6. Must be easy to use.
SURVEY v2.30 can cope with a survey of up to 9999 stations and 16250 legs (complicated networks tend to have more legs than stations). Up to 2000 junctions with 3333 closed traverses can be solved simultaneously (larger maps can be solved in overlapping sections), and the program can be run on a standard PC without the need for extended memory (although a hard disc is needed and a colour screen helps). Accurate hardcopies can be plotted with the data viewed from any angle using HPGL (Hewlett Packard Graphics Language) plotter output.
The survey information is entered using
an interactive menu system which prompts the user for the required
data and checks it for nonsensical values as it is entered. This
makes the program much easier to use than programs which need
text editors to enter the data, and unfriendly and difficult-to-remember
commands to run them (many users do not have an in-depth knowledge
of DOS). The data can be plotted on the screen as each leg is
input if required.
Each time a closed traverse is measured there will be a finite closure error. With a complicated network of many junctions and traverses the task of distributing the closure errors in an optimum way becomes impossible without the aid of a computer. The key to solving the problem is deriving equations which relate the positions of the junctions to one another and solving these. The method used in SURVEY v2.30 is explained below:
Consider part of a large network:
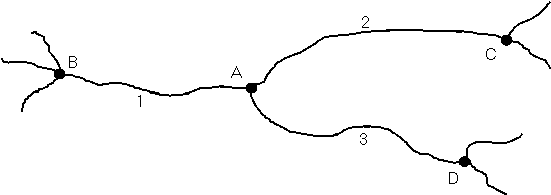
The coordinates of junction A can be determined by adding the x,y,z offsets of traverse 1 to the coordinates of junction B. Alternatively, the position of A could be found from the position of stations C or D and the appropriate traverse offsets between them, ie:
PA' = PB + V1 or PA' = PC + V2 or PA' = PD + V3
where PA' is the new position in 3 dimensions of point A, PB the current position of point B, and V1 is the measured vector between B and A, etc.
Unfortunately, the three equations above will yield different answers because of the measurement errors in the three traverses and errors in the positions of points B, C and D.
One solution is to calculate the position of point A from the average of the three choices:
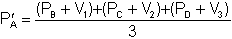 (i)
(i)However, this method assumes that each traverse has the same accuracy and is therefore of the same importance when considering the position of A. In reality this is not likely to be the case. Each leg of the traverse will tend to have random errors brought about by instrument inaccuracies, instrument reading difficulties and station position errors. These should be relatively small but the cumulative effect may be significant on a traverse of many legs. Irwin and Stenner1 published results which related actual data from traverses in St. Cuthbert's to the predicted traverse accuracy from statistical considerations. The evidence from the study was that the traverse error is related to both the length of the traverse and the number of legs in the traverse. It is therefore important to decide how accurate all the traverses are likely to be when using them to locate the optimum junction positions (note that this theory assumes that there are no gross errors - more about this later).
SURVEY v2.30 determines a weighting for each traverse using statistical considerations (discussed later in this article) so that equation (i) is modified to become:
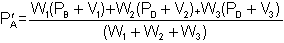 (ii)
(ii)where W1 is the weighting of traverse 1, etc.
Similar equations relating each junction
to its neighbours can be derived for the whole network, and these
must be solved as a set of simultaneous equations (one for each
junction).
SURVEY v2.30 calculates the weighting (W) for each traverse based on a combination of a user defined weighting (WU) and a statistically derived weighting (WS). The user defined weighting is simply a value from 0 to 5, with 5 being the default of fully weighted. A lower weighting will cause the traverse to have proportionally less influence on the 'fit', and a zero weighting will discount it altogether. In this way the user can de-weight any traverses which he considers to have been measured to a lower standard or where it is likely that a gross error was made. The statistical weighting is the expected Variance (Standard Deviation squared) of the traverse based on the accuracy standard chosen (the program defaults to values suggested by BCRA grade 5). The user and statistical weights are combined to generate the overall weighting according to:
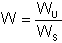 (iii)
(iii)Thus the weighting of the traverse is inversely proportional to its variance.
The Variance of the traverse is calculated by summing the variances of each individual leg of the traverse. SURVEY v2.30 calculates a separate variance in each of the X,Y and Z directions because the accuracy of a traverse is likely be different in each direction (for instance, if the compass error is large relative to the taping error, then smaller errors would be expected in the direction of the traverse than perpendicular to it). The traverse variance is calculated as follows:
Let: STE = Station position error - (value equivalent to 1 standard deviation)
TPE = Tape measurement error - (1 s.d.)
ANE = Angular measurement error in radians - (1 s.d. for both compass and clino)
These values are selected by the surveyor perhaps from the BCRA grades. Note that 99.9% of all measurements should fall within limits of ±3 s.d. for a normal distribution and this can be taken as the maximum expected error.
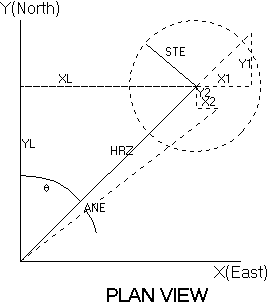
Consider the vertical and projected horizontal errors of a leg:
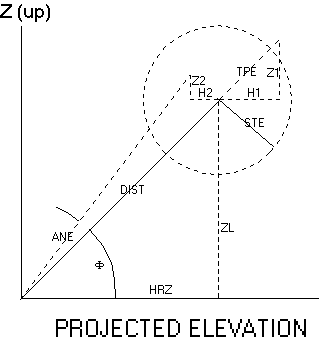
|
DIST is the measured leg length f is the inclination ZL is the vertical leg offset = DIST.sin f HRZ is the horizontal component = DIST.cos f Z1 is the vertical error due to tape error Z2 is the vertical error due to clino error H1 is horizontal error due to tape error H2 is horizontal error due to clino error |
The maximum vertical variance VZ is the sum of the individual vertical variances:
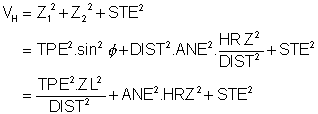
The maximum horizontal variance VH due to vertical errors:
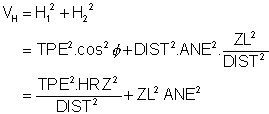
Resolve VH into variances in the X and Y directions VX and VY :
|
q
is the bearing XL is the easterly leg offset = HRZ.sin q YL is the northerly leg offset
= HRZ.cos q
X1 is the easterly error due to vertical errors X2 is the easterly error due to compass error Y1 is northerly error due to vertical errors Y2 is northerly error due to compass error |
For a complete traverse of n legs the
variances of the legs are summed to give the total variances in
each direction:
These are each substituted into equation (iii) in place of WS to produce the traverse weightings in the three directions.
Classical methods of solving the simultaneous equations (ii), such as Gaussian Elimination, can be used where the number of simultaneous equations is low (less than 100 say), but these methods are not suitable for highly complex networks such as Box Mine or some of the large maze-like caves around the world. In such cases it is necessary to adopt an iterative technique as these yield more accurate results, faster and with a lower computer memory requirement.
A simple iterative technique is to apply each simultaneous equation in turn to calculate the new position of each junction using the current positions of its neighbours, and to work through all the equations one by one. If this process is repeated over and over again, the junctions will gradually move less and less for each iteration and will settle towards the true simultaneous solution. A good solution is judged to be reached when no junction moves by more than a specified tolerance during an iteration. This is called the Gauss Siedel iterative method, but is fairly inefficient and inaccurate for complex networks. SURVEY v2.3 currently uses a modification of this method which gives much faster convergence and better accuracy, called Successive Overrelaxation (SOR). This is achieved by computing the movement of a junction due to an iteration using the Gauss Siedel method and increasing this by a factor to accelerate the movement. For SOR equation (ii) for point A becomes:
If PA
is the current position of A and PA'
is the new position calculated from Gauss Siedel then:
For SOR the movement is increased by
a factor R so that:
This method is found to be stable for values of R such that: 0 < R < 2. In practice, values around 1.95 yield good results. SURVEY v2.30 currently judges convergence to be when no junction moves by more than 7mm during an iteration.
After the simultaneous equations have been solved to optimize the junction coordinates, the distortion of each traverse can be calculated and compared with its expected tolerance limits based on the accuracy values chosen. SURVEY v2.30 redraws the map on the screen with the traverses coloured according to their distortion. Green is used where the error is low (less than 1 s.d.), white is used for acceptable errors (between 1 and 3 s.d.) and red is used for errors greater than 3 s.d. (ie outside expected limits).
If the majority of the traverses show as red, you are kidding yourself about the standard of your measurements and the accuracy limits set in the program should be increased. With a mixture of green and white traverses and the occasional red traverse the map generally reaches the standard that it is being judged against. In this case the red links are those which are most likely to contain a gross error, and in an ideal world they should be re-surveyed. However, this may not always be possible and so SURVEY v2.30 allows the user to de-weight these traverses and re-optimize the map. De-weighting a traverse effectively increases its expected variance and therefore both reduces its influence on the fit and increases its allowable distortion. By de-weighting the bad traverses sufficiently to produce a plot with no red traverses, I believe that one can be reasonably happy that one has done the most that is possible with the data. Once an optimized solution is accepted, the stations along the traverses are positioned by distributing the traverse distortion amongst the legs in proportion to their length. Finally, the open traverses (which play no part in the optimization process) are re-positioned.
6.0 BOX MINE SOUTHERN SURVEY
As mentioned above, the program was written to solve the problems of the latest part of the Box Mine survey, and this project has largely been the driving force for the continued development of the program (although it is currently being used on several major cave surveying projects in the UK and abroad). The Box southern region survey is now nearly complete and I am gradually also entering data from the central area survey into the database. There are now 3562 stations of which 745 are junctions of closed traverses, 4538 legs in a total of 1174 closed traverses and several hundred open traverses. I estimate that about half of the total Box data has been input so far, and so the program should have sufficient capacity to handle the complete system.
The program has shown that the standard of our surveying is increasing as time goes on. There are far fewer bad fits in the newest data compared with the oldest. The main reason for this is that the program has forced us to be more disciplined in our surveying and caused us to mark the station positions accurately (with cairns not paint!). A great benefit is that the entire survey can be plotted in only a minuite or two on an office laser printer and a large scale print of the section being worked on can be quickly plotted ready to be taken underground on the next surveying trip.
7.0 ACKNOWLEDGEMENTS
I would like to thank Dave Irwin for his comments which have helped me to develop the program and Bob Thrun for his assistance with the mathematics.
8.0 REFERENCES
1. Accuracy and closure of traverses in cave surveying, D.J. Irwin and R.D. Stenner, Trans. British Cave Research Assoc., Vol. 2, No. 4, pp 151-165, December 1975.