Snippets
Surveying for Rescue - D.Merchant
What is needed in a survey for rescue purposes.
Blunder Prediction - Larry Fish
The detection of blunders & ranking of likely fixes
Blunder Discussion - Larry Fish, Olly Betts, Wookey
Further discussion of blunder prediction issues
WinKarst - Garry Petrie
Thank you to those who have set pen to paper/keyboard this issue. Please remember this is your journal. If you have anything to say about surveying - what you are doing, things you see here that you agree with or disagree with, please write to the editor about it.
I am also very keen to organise some field meets for the surveying group, but don't have time at the moment. If anyone else feels enthused, please step forward - it's not that hard. Just pick a weekend and a caving area, book a hut and tell everyone.
Tim Long
Morgannwg Caving Club has published a survey of Ogof Draenen. The survey is £3 plus P&P and consists of a grade 2/3 line survey, enhanced with passage widths and in two colours for clarity. For your money, you get two sheets of survey, one showing the whole cave and one showing an enlargement of the complex central area. There is also a description on a separate sheet of A4. There is a grade 5 survey in progress, but this is not expected to be complete for at least two years.
The survey was produced using Survex and Corel Draw. The HPGL plotter driver was used to produce an output file which was then imported into Corel Draw to enhance the passage widths and add colour, OS grid marks, titles and so on. A useful feature of the Corel Draw! importer is that it seems to "group" the lines into something remarkably close to passages. This is a fortunate side effect of the way that PRNTHPGL generates its plotter output. The finished product was then professionally printed in red and black. The result is a remarkably usable line-survey which is adequate for navigation around the cave (particularly the round trip, which has caused a lot of confusion).
Surveys can be obtained from Alastair Garman on (01222) 864291 (day) or (01222) 751100 (eve) or write to him at 38 Briarwood Drive, Cyncoed, Cardiff, CF2 6SR.
Alastair does NOT deal with access enquiries, they are handled by me. The surveys are also available from Dragon Caving Gear and have been offered to all major caving retail outlets.
The cavers archive (where all caving software can be downloaded from, and the Caver's digest discussion list is archived) has found a new home:
The ftp address is:
In oldspeak: chert.lmu.ac.uk /pub/chert
In newspeak (URLs) ftp://chert.lmu.ac.uk/pub/chert
Nigel Armfield at Leeds is the new keeper. Mailto: N.R.Armfield@lmu.ac.uk.
On the weekend of April 19th, CREG held a Field Meet in the Forest of Dean. The details of this where relevant to Radio etc. are in the CREG Journal. Here I will just mention the surveying aspect. We were given a very thorough explanation of GPS systems by Philip Mattos, an engineer at Bristol University who has worked for Inmos & SGS Thompson on cheap, but effective GPS. Expect an article on the sordid details of GPS systems and how well they actually work when used to help with entrance locations, in the near future, as well as a review of the extraordinarily cheap but capable Garmin 45.
The NSS Surveying & Cartography Section has produced a new issue of their journal after a long hiatus, due to two changes of editor. The new Editor is Pat Kambesis, 2466 Drew Valley Rd, Atlanta, Ga 30319. The last issue was produced over 18 months ago.
This issue contains the following:
Minutes of the 1994 Surveying and Cartography Section Meeting, Bracketville, Texas: Mostly the sort of dull stuff you don't want to know, but it worth noting that the SCS has 143 members, and $2817 in the bank [! -Ed], with about $900 of that earmarked for issues of C&T already paid for by members.
1994 NSS Cartographic Salon: The SCS organise a survey-judging salon at their annual conference, just like the photo & video competitions we have in the UK. It would be nice to do the same at BCRA conference (anyone fancy organising/judging it?). There were 58 entries from 32 entrants, covering Belize, Dominican Republic, Guatemala, Mexico, China, Switzerland & the USA. This is also the first year that electronic 'computer only' surveys were entered. These had to be left un-judged for this year, as the judges had no suitable criteria for comparing them to each other, never mind paper surveys. The overall winner was Pat Kambesis's survey of Wu Dong, Gizhou, China.
Protecting Suunto Instruments: All about how to dip your suuntos in thermoplastic rubber, to give them effective protection from the cave. They need to be sealed first with silicone to stop the fumes fogging up the lens, and the viewing window covered. Then you dip and dry the instrument three times to get a good even coating, which will not split at the corners.
The OTR Compass Course OR the need for Compass Courses: OTR is 'Old Timers Reunion', a big bash for old cavers. They have a fixed survey course there which has been used for a number of years. Collecting the last six years results allowed an analysis of the variation in instruments. Of the 167 sets of results, 150 were done with Suuntos, 11 with Sistecos, and 6 with Bruntons. The average errors were as follows:
| Instrument | Compass | Clino |
| Suuntos | 1.016 | 0.395 |
| Sistecos | 1.470 | 0.449 |
| Bruntons | 1.710 | 0.512 |
Showing that compasses have 2-3 times the variability of clinos, and that Suuntos are more accurate than the other instruments.
Cave Survey Standards for Carlsbad Caverns National Park: CCNP includes Carlsbad Caverns, Lechuguilla Cave, and many others. The Park Authorities have produced a strict specification that surveyors must work to.
Membership List
Guy van Rentergem has produced a new version of his clickable cave database. There are now versions for Belgium & Jamaica.
It has been re-written in Powerbasic, for greatly improved speed, and has improved zooming in 5 levels, with the bottom level automatically giving a list of caves currently visible. This is a handy piece of software that could easily be adjusted for use in any area. It is available from Wookey or the cavers archive.
GvR writes:
The symmetrical pattern you see when you are zooming in the Jamaican program is caused by rounding errors in the conversion of the older Imperial co-ordinates to the newer metric JMG co-ordinates.
The datafiles are now dBase files so the data is more universal than the older ASCII files. The programs are also re-written in Power-Basic. A fine language. And I hope all the bugs are killed now.
D. Merchant, Casualty Officer, BRCS CMRT.
The production of cave surveys often seems to be entirely for the benefit of future cavers -in the manner of an underground holiday brochure. Whilst it is indeed that surveys finding their way into guide books do mostly serve this purpose, there are other uses, often requiring specific extra information to be included. Rescue work falls into this category.
The production of ' logistic ' surveys is a surprisingly well hidden corner of survey work - one of the few areas where the surveyor hopes his handiwork is never used!
A logistic survey differs immensely from the guidebook survey we are all used to. It serves a specific and specialised purpose - that of enabling the best route for removal of trapped casualties to be determined, whatever their medical condition or the weather. The system of logistics surveying used by us codes each and every part of the system with a two-figure number detailing the type of casualty that can be passed through that section feasibly, and the specific hazards such as stability and flooding.
I won't run off into pages of code lists, but for example a passage denoted 4.3 would be suitable for passage of a casualty with a splinted leg but not one in a stretcher, and is liable to flood unexpectedly. It must be considered in making these classifications that cavers may only take an hour to exit a cave but a casualty may take eight times longer to be hauled out.
Surveys actually in use during rescues exist in the form of a system plan showing all passages, sumps, pitches, exits but limited detail. This serves a vital purpose in locating the casualty, when often the caver who has raised the alarm can show on this plan where they are, or can remember " they took a low passage third left past the sump ". Often in 'simple' systems no detailed plans are required, but for more complex caves a set of detailed section plans are kept showing passage sizes and distances between passages in case a dig-through is required. Additionally a textual description of all passages is kept detailing specifics such as the presence of anchors, escape traverses, floor material, watering, etc. The last two are of particular importance - a crawl in a passage 3ft high with a foot of water in it is easy for uninjured cavers, as the head is highest when crawling. Strapped to a stretcher which does not float, your nostrils are only eleven inches off the floor.
Cross-sections are given a great deal more often than for guidebook surveys, and additional details never seen normally are extensively used : depths below ground level and overlying rock types. This information is vital if a total collapse forces an emergency dig from the surface. Digging down towards a high rift will save hours of work but not if it's under a lake.
Structural integrity is also detailed in a different way due to the extra loads placed on belays or traverses by the weight of the casualty, stretcher and team members. Details of the system's response to seismic activity are given both for blasting purposes and in case of earthquake (yes, we do get them in Britain, and yes, they do cause caves to collapse.)
At present, the surveys are kept in paper form, with a ring-bound laminated set in the ambulances for use on-site. However, we are in the process of computerising the records to ensure that all surveys are easily up-datable. It is the hope to store the local systems on a laptop so that viewing packages - such as Survex's CaveRot - can be used on-site to wander through the system. If the team then find a new fall, or insert a new traverse line, the survey can be updated as soon as they return. The current time-consuming job is building the front end to tie together text files with extensive notes about a particular passage to the maps of said passage. The idea is that you click on a passage or pitch-head and up pops the watering, stability, rigging details and all in the corner of the screen. All we would then need is an icon to turn off bad weather!
The best way to see what a log survey looks like is to look at one. However, since this article is coming to you via VMS email, pretty piccies are out of the question. But here goes with the accompanying text for the entrance crawl
of OHF ( Poacher's Cave ) in the Alyn valley, N. Wales, to show what sort of things we want to know......
| SJ 19102 65504 | Limestone vadose active partially floodable risk E4 | |
| Ent. Alt. 480ft | L 2624ft | Ser. No. 589576897 |
ENT: Rectangular crawl linear & horiz 170 mag for 10ft @ 2.5'x2.5' C6.0 over mud to steel door 2'x2' opening out and right. Crawl continues 10ft @ 2.5'x2.5' rising at 20 deg dirn 170 mag C7.0 over mud. seismologic risk minimal, flood risk zero, infill risk minimal
Crawl bears 150 mag opens into rift ( Dyers Adit) 12ft high, 3ft wide. Roof calcited choke - top accessible from main Dyers Adit passage. Seismological risk medium, infill risk medium, SWL 500kg. Clearance to ground above choke 16ft under woodland ( limestone)
CAUTION:
floor is steel planking with central manhole (covered) 24"x24".
C6.0. Floor SWL 300kg. 2x8mm anchors on wall 3ft above manhole
SWL 1200kg plus two CRO 10mm anchors roof level 10ft above manhole
SWL 3500kg.
Ahead bearing 175 mag over +5ft boulder fill is main Dyers Adit passage. Manhole covers 15.5ft rift pitch-vertical, width 28" at top opening to 3ft at floor (sand). Pitch haul time 30 seconds, C6.2. , ropes 50ft. Pitch always dry. Limited space around manhole so stretcher haul MUST use higher 10mm anchors to clear it.
Foot of pitch has theoretical flood risk of +12" in exceptional conds.
.... the survey continues but this extract doesn't ......
Larry Fish
Closing Loops in surveys has long been a subject of debate amongst surveyors. It is often necessary for drawing-up, and distributing errors is a good thing, so long as those errors are only the ones expected to be generated by the survey method's limitations. As soon as there are cock-ups in a loop, then simply distributing that error is not a good thing to do. What surveyors need is for the software to tell them when a loop does not close within the expected error, and perhaps even to highlight the legs likely to be responsible for the error. Obviously this is not an easy task, but there are techniques that can be used, and these are starting to be addressed by software authors. The term Blunders has come to be used to distinguish these major errors from smaller systematic & random errors.
This letter from Larry Fish was prompted by his reading of a pile of collected info on loop adjustment & analysis collected by Wookey & Olly Betts.
One of the topics that I found very interesting was the idea of locating blunders. In the early 1980s I came up with an idea for locating blunders. The idea worked like this: if you had a blunder in a loop it would leave a unique signature on the error vector. If for some reason, you knew where the blunder was, adjusting that measurement for best results would significantly improve the loop error. If you attempted to adjust any other measurement, the improvement in the error would not be as dramatic.
The actual technique involved in adjusting each individual survey measurement (azimuth, length and inclination), one at a time, for best closure of the loop. The theory is that the adjustment that best fixes the closure error would be the blunder. I don't know if this is that same technique that Bassham describes in his article, but I am in the process of trying to track down a copy of his article to see.
[Elbert Bassham's article, (NSS Bulletin, Volume 41, Number 1, January 1979) gives a thorough treatment of which blunders can be detected in compass & tape, and theodolite loops - Ed] In the early 1980s, I wrote a program for the Apple to test this idea. At the time it seemed to work pretty well, but I didn't take it very far. As a result of reading the materials you sent me, I have revived the program and converted it to the PC. It seems to work fairly well for loops that contain a single blunder. It appears to work for more than one blunder, but the results are less clear. Currently, the program lists the ten best fixes for each loop. I'm exploring other ideas like iteratively locating blunders and progressively removing the larger ones until the error falls below some specified value.
I thought you or Olly or others might be interested in this idea and might offer some mathematical insights or constructive criticisms. The results seem pretty clear when you have one blunder. When there are multiple blunders, the results are confusing. Currently, I rank order the fixes by lowest residual loop error, but I wonder if this is valid. For example, lets say you have two potential blunder adjustments that seem to fix the closure error fairly well. One requires 180 degrees of adjustment and the other only requires 2.5 degrees of adjustment. Which is the better choice? Or, lets say you have one the requires 10 degrees of adjustment and one that requires 5 meters of adjustment. Is it valid to compare angle and length adjustments? It also seems to me that there is a sort of a signal-to-noise-ratio problem where the blunder "signatures" eventually get overwhelmed by random measurement error "noise."
I have included a copy of an article I wrote which appeared in "Rocky Mountain Caving" in 1986. It describes the technique for adjusting shots in detail. [By the time you read this, the preliminary software using these ideas should be available at the cavers FTP sites]
The following article is an excerpt from an article called "The Program Groaning Wrote" that appeared in "Rocky Mountain Caving" Autumn 1986. It has been updated slightly for readability and accuracy.
In 1979 I starting working on a project to computerise the survey data for Groaning Cave. The cave had been discovered in 1969 and I was suddenly handed ten years of survey data that had never been processed by a computer. The early surveyors had processed all the information by hand and as a result, there many anomalies and problems in the data.
When I looked at the Groaning data, I found that many loops near the front of the cave had large loop closure errors. Luckily, I had more than one survey for some of the worst loops and was able to compare good surveys to bad surveys of the same passage. Much to my surprise, the errors in the surveys were not due to the accumulation of small, random errors; but were due to major blunders like reading the wrong end of the compass needle, transposing digits on the survey notes, mixing up azimuth and elevation, etc. By comparing good surveys to bad, I could easily fix a bad survey by repairing the worst blunders one by one until the survey closed.
As I played with the idea more, I discovered that I didn't always need a good survey to find the blunders in a bad survey. I could see that each blunder leaves its own special mark on the closure error. For example, an azimuth error has no effect on the vertical component of the closure error, so a compass error can never produce a vertical error. If you have a survey with one blunder in it, the blunder will produce a very specific kind of closure error. By going through the survey and adjusting each measurement in turn, you will find that one of the adjustments will close the loop perfectly and this will be the blunder. If there are multiple blunders, there will be several adjustments that partially fix the error. The best fixes correspond to the worst blunders.
The basic closure process consists of making test adjustments of each measurement in every shot. For each measurement, there will be a certain adjustment that will be the best closure possible for that particular measurement. As we adjust each measurement, we keep track of the most successful adjustments. The best adjustments will always correspond with the worst blunders.
The trick to this technique is to find simple routines that calculate the best adjustments for azimuth, inclination and length measurements. The following section describes the algorithms for finding the best adjustment for each measurement.
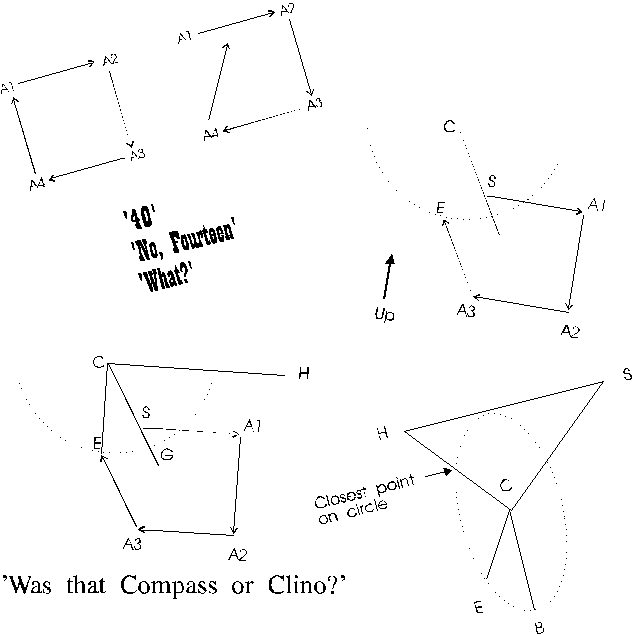
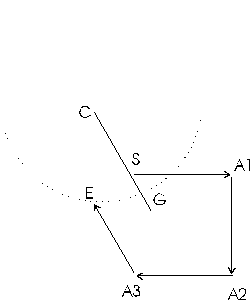
Figure 3 represents a closed cave survey loop. Point S is the start of the survey, point E is the end of the survey. The angle at A1 is the angle we are going to adjust. The object is to find how much to change angle A1 to produce the best closure.
If we rotate angle A1 through 360 degrees, point A2 will describe a circle whose radius is equal to the distance between point A1 and point A2. Since the azimuth angle measurements in cave surveying are referenced to magnetic north, point A2 tends to be a hinge point. That is, as A1 is rotated, the angle at A2 also changes but every angle at every shot from A2 to the end of the survey stays the same. As a result, as A1 is rotated, E describes a secondary circle whose centre is offset from A1.
The secondary circle is important because it represents all possible points that E can occupy as we adjust angle A1. Thus, the best closure must be somewhere on it's circumference.
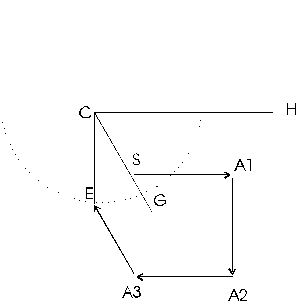
In figure 4, C represents the centre of the secondary circle. This centre C is located by taking the offset between A2 and E and adding it to A1. To find the best closure, we must find the point on the circle that is closest to the starting point S. Since the shortest distance between any point and a circle must be on a radius, the best closure must be at the point where the line C - S intersects the circle.
We know the locations of S,E,A1,A2,C and the radius, so all of the remaining points and angles can be calculated from this information.
In figure 5, we construct a horizontal line from C to H; and using point S, we construct a right triangle. The location of G, the point of best closure, can be located using the triangle and polar co-ordinates. The new closure error is the distance between G and S, and the adjustment angle is the difference between angle G-C-H and angle E-C-H.
Adjusting length is more complicated because the shot length has both the azimuth angle and dip angle effecting it. As a result, the shot length is actually a vector in three dimensional space.
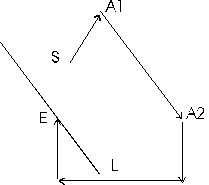
Adjusting a particular shot for best closure is, in some ways, similar to adjusting azimuth. For example, figure 6 represents a plan view of the survey, where S represents the start of the survey and E the end of the survey. The survey has a large survey error. If we attempt to minimise the closure error by adjusting the shot length of A1-A2, point E will move, drawing line L which represents all possible adjustments of the shot. Obviously, the best adjustment will give the shortest distance between point S and line L.
Since we are working in three dimensions, it is easiest to work using vector algebra. The shortest distance between a point and a line in 3-D space is given by the following formula:
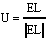
Adjusting the dip angle is the most difficult part of the closure process. Since it is an angular adjustment, it is similar to the azimuth adjustment except that it takes place in three dimensions. This is because the inclinometer is free to rotate around the vertical axis, where as the compass is always held in the horizontal plane.
Figure 7 is a profile plot of a survey. The vertical or Z axis is toward the top of the page. Point S represents the start of the survey and point E represents the end of the survey. As you can see, there is a closure error between S and E.
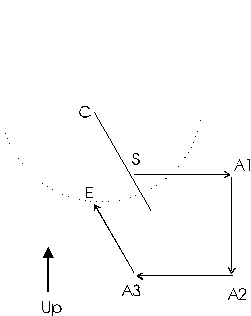
In this example, A1 will be the dip angle that will be adjusted. As with the azimuth adjustment, when A1 is rotated through 360 degrees, A2 describes a circle with A1 as the centre. Since all of the shots from A2 to E remain unchanged, as the adjustment is made, A2 will hinge and E will move through a secondary circle offset from A1. Since the secondary circle represents the result of all possible adjustments, the best closure must be some point on the secondary circle. The task is to find the closest point on the circle to the starting point S. This will be the best possible closure we can attain by adjusting the dip angle at A1.
Since the secondary circle and the starting point S are in three dimensions, the process of finding the closest point is more complex.
Figure 8 represents a three dimensional view of the secondary circle. Point S is the start of the survey and point E is the end of the survey.
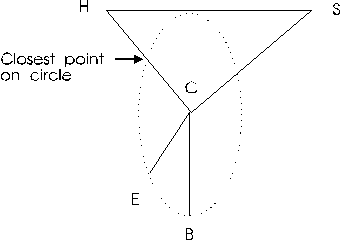
The strategy for finding the closest point on the circle to S is to find the closest point from S to the plane of the circle. In the diagram, H is the closest point in plane of the circle to S. Now we calculate the intersect between H-C and the circle. This will be the closest point to S and will represent the best possible adjustment for this shot.
Since we know the location of E and can calculate the location of B and C, this gives us two vectors in the plane of the circle: C-B and C-E. By taking the cross product of CE and CB, we get a vector perpendicular to the plane. Taking the dot product of C-S and the unit vector of the perpendicular, we get the distance between S and the closest point on the plane: point H. Adding a perpendicular vector of length H-S to the co-ordinates for S gives us the co-ordinates for point H. With these co-ordinates, all other co-ordinates, angles and distances can be calculated.
Larry Fish, Olly Betts, Wookey The ideas in Larry's letter & article above, prompted some interesting discussion on implementation & detail. The following is adapted from the resulting 3-way Email correspondence.
| Olly: | My only comment is that the signature of a blunder isn't necessarily unique. In our Austria data, we have a number of plumbed legs for pitches. A tape blunder in any plumbed leg in a traverse (or string or whatever you call it) will be indistinguishable from the same length blunder in any other plumbed leg in that traverse. |
| Larry: | In my test loops, there are several situations where two shots will represent the best fixes and thus make the signature non-unique. |
| Olly: | Is this just due to the "noise" level of random errors making it impossible to decide which fix is better, or are the signatures of the fixes (anti-blunders) actually identical too? I would suspect the latter is very rare, but I might be wrong. |
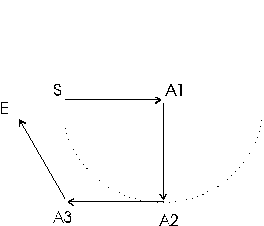
| Larry: | I don't know how rare it is. In very simple test caves
it is fairly common. For example:
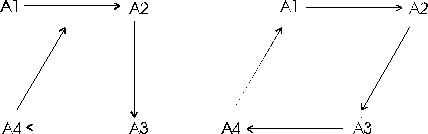 If you have an azimuth blunder between A4 and A1, the blunder program see two fixes. The first one occurs when you adjust the angle at A4 the second occurs when you adjust the angle at A3. I suspect that as the loops get more complicated, the chance of the "antiblunder" goes down. |
Typical blunders: | |
| Wook: | This is obviously an inexact science. I believe that most blunders fall into a few common categories - digit transposition, reading 172 as 168 (easy with Suuntos), reading percent instead of degrees on a clino, & misheard values (50 instead of 15). Any blunder analysis should also check for systematic errors (e.g. clino zero error, or tape missing 20cms off the end.) This involves applying the same fix to all shots, as opposed to just changing one or two shots. |
| Olly: | This is a good point, and will allow some decision about
the 'best blunder-fix' to be reached in many cases. Say my misclosure
is almost exactly 35 feet vertically. Then it's much more likely
that this 15 foot plumb was actually 50 feet, than that 32 foot
plumb was 67 feet.
It would be interesting to find out what the common styles of blunder are. Presumably it's language specific amongst other things. 15 and 50 sound very similar in English and German, but much less so in French. Also, a cave full of rushing water will probably make these errors more likely, whereas a slightly dyslexic survey note-taker (CUCC has had one of these) will make transposition errors more likely. Looks like we'll need to add "language spoken by survey team", "background noise level of cave", and "dyslexicosity of survey note taker" to HTO to do this properly...:-) |
| Larry: | I've seen examples of common/systematic errors show up with the blunder program. For example, I noticed one loop where the best fixes were all azimuth corrections of about 13.50 degrees. The number 13.50 happens to be the magnetic declination for this area. Also, the surveyors where using Brunton compasses which have an adjustment for declination. I think that part of the loop was done with the declination set to zero, and part done with it set to 13.5 degrees. |
How can you rank likely blunder fixes? | |
| Larry: | The results seem pretty clear when you have one blunder. When there are multiple blunders, the results are confusing. Currently, I rank order the fixes by lowest residual loop error, but I wonder if this is valid. |
| Olly: | For a one blunder fix, any fix which doesn't get you inside
95% confidence level for the random errors is probably a no-hoper.
In case you or Wookey aren't clear on this, xx% confidence is
the range of values for which there is an xx% probability that
the value will lie inside that range.
Assuming a normal (gaussian) distribution:
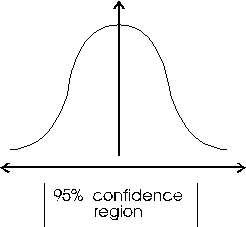 The horizontal axis is the value, and the vertical axis is the "probability density" of each value. 95% probability is between 2 and 3 standard deviations of a normal distribution if I remember correctly. There's only a 1/20 chance that random errors could land you outside this range. Maybe 97.5% would be preferable (3 s.d.-s?) i.e. a 1/40 chance. If no one fix gets you in the confidence region, then it's time to look for a 2 or more fix solution. |
| Larry: | For example, lets say you have two potential blunder adjustments that seem to fix the closure error fairly well. One requires 180 degrees of adjustment and the other only requires 2.5 degrees of adjustment. Which is the better choice? Or, lets say you have one the requires 10 degrees of adjustment and one that requires 5 meters of adjustment. Is it valid to compare angle and length adjustments? |
| Olly: | If you assume a variance/standard deviation on each measurement, then you can sort of compare them by asking how many s.d.-s each blunder is. However, this is probably not very useful, as blunders probably aren't proportional to the measurement in any direct way. In terms of fixing a blunder incorrectly it would be preferable to make a smaller change though. |
| Larry: | It also seems to me that there is a sort of a signal-to-noise-ratio problem where the blunder "signatures" eventually get overwhelmed by random measurement error "noise." |
| Olly: | As you say, in general the signatures are unique (apart
from a few cases, as I said above). If you visualise them as
a space, there's a "fuzz" around the blunder, which
is equivalent to a "fuzz" around each possible fix and
the blunder being a single point. If the point is within the
fuzz, you have at least one fix, if it is outside, you don't have
a good single fix. The size of the fuzz is the confidence region.
Wook's common-errors concept is a very useful idea. The hard bit is to make a list of such errors and get some code to weight in favour of fixes which are covered by one of them. What this does to the space is to change the fixes from being circles and lines, covered in fuzz, to being point on those circles and lines, each point with fuzz. Blunders in systems with interlocking loops will need some thought. In some ways it is easier, as the additional loops give you something to compare against. However, fixing a blunder in one loop will subtly affect others. |
Will Internal angles help? | |
| Larry: | I sent John Halleck some information about what I was doing, and he had a very good suggestion that will help narrow down the location of the blunders. He pointed out that the sum of the interior angles of a loop should total some multiple of 180 degrees. If they don't, you know that there is an error in one or more of the azimuth measurements. This could be could be combined with other blunder information to narrow the likely blunder candidates. I think I may be able do something similar with inclination angles. |
| Olly: | This is only useful for things like theodolite surveys,
where the difference in angles is measured. For a tape/compass/clino
(or tape/compass/altimeter) you will always get a multiple
of 180 degrees. Here's why:
We have a loop of n legs. The bearing of leg i is B(i) degrees. 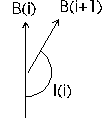 I(i) + (B(i+1)-B(i)) = 180 degrees So I(i) = 180 + B(i) - B(i+1) (And closing the loop, I(n) + B(1)-B(n) = 180 degrees). So adding the internal angles: I(1) + ... + I(n) = (180 + ... + 180) [n times]
- (B(2) + .,, + B(n) + B(1)) |
| Larry: | If you have a choice between a length and an azimuth fix, this would narrow your choices. I think something similar can be done with inclination angles. |
| Olly: | For a similar reason, I believe you won't get anywhere except for surveys where you measure the difference in inclinations at each station. |
| Wookey: | Does this not only show that after adjustment you will always get 180*n degrees? |
| Olly: | No, I've just done the sums with the bearings as read, not any adjusted form of them. I believe you will always get 180*n. In fact the ends of a blundered loop won't meet, but this won't affect the sum of the internal angles calculated as if it did (and I can't see any other way to calculate them). |
| [ Long discussion, with Wookey being a bit dense and arguing that the angles won't sum to 180 * n if there is a blunder ] | |
| Larry: | Olly, I think you are right! I kept thinking
that if you blunder one azimuth, it only changes the one internal
angle, thus changing the sum of all the internal angles by the
amount of the blunder. I didn't see that if you blunder one azimuth,
it changes two internal angles. The angle at the current station
and the angle at the next station. For example:
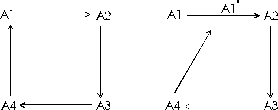 If the shot between A4 and A1 is blundered the angle at A4 and A1' both change in complementary ways. Thanks for pointing this out. John Halleck must have been thinking about land surveys when he made the suggestion to me. I regard him as the guru of loop closure errors and didn't examine the concept very carefully. |
This quarter we only have a new release of WinKarst, and the Compass 'Home Companion', which it looks like there isn't space for this issue.
Garry Petrie
WinKarst is the most extensive and fastest cave mapping software written for Windows to date. It has been verified with complex cave systems with over 18,000 station. Because the program does not contain a method to enter survey data, it may be freely distributed as freeware. However, the raw data format is ASCII and survey data files can be created with any text editor. The program is distributed with sample cave data to get the user started. User feedback would be greatly appreciated.
1. Improved printing. WinKarst now includes a print preview operation in which the user can view what will be printed before it is actually printed. Since the aspect ratio of a Window will generally not match that of a standard piece of paper, this function is useful for seeing what else will be printed in a close up views of the cave. Note that autoscaled plots will always fill the page, depending on the paper's orientation. Printing in the previous release of WinKarst would only fill the page if the Window was maximised.
2. Expanded support for multiple caves within a cave survey. All of the caves in a system can now be plotted in relation to each other in the same window. The entrances or control points in each cave can be labelled and each cave can be give a unique colour. Double clicking near an entrance symbol brings up information about that cave.
3. Three layers of hierarchical objects, systems, caves and surveys. Each object can be viewed separately in its own window. For example, the user can have one window with the entire cave plotted and another window with only a single survey in that cave. The mouse's focus only applies to the object in the window. For example, double clicking near a station in a survey window will only cause a search of station locations within that survey, not the entire cave. Colour by depth is applied to the extent of the object, i.e. survey, cave or system. The co-ordinates reported in the status bar will jump as the mouse passes from window to window.
4. WinKarst now comes with extensive help system. The help system is context sensitive, cross linked, includes keywords for searching, has browser sequences and bitmaps with hot points for complex functions. The help pages are printable and include the descriptions of both the raw ASCII and binary data file formats.
5. The user interface has been revamped. The old textural representation of the cave is gone, as are the complex pulldown menuing sequences. Each of the programs main controls for objects, e.g. caves, stations, loops, etc. are now access through dialog boxes. It is no longer necessary to select an item, repeat and repeat to enable the desired choices. The user now can check boxes and push buttons in a single dialog before returning to the map. Keyboard accelerators remain for main functions. Most of the dialogs contain a list of the objects in the cave, surveys for example. The user can pick a name in the list and learn about it by pressing the Info button or see what colour it is in the colour box. The dialogs can be operated with either the mouse or keyboard.
WinKarst may be obtained by one of three ways. WinKarst is available from either of the popular caving Internet ftp sites, chert.lmu.ac.uk or speleology.cs.yale.edu. The Internet can be accessed through many of the online services such as CompuServe and America Online or though many direct corporate or university connections. Two, for those people who are willing to risk the email system and understand MIME encoding, I will email it to them (a one meg plus file). Contact me at gp@ssd.intel.com. Finally, three, by surface mail. To obtain a copy by surface mail, send $5 to cover postage and materials to: Garry Petrie, 19880 NW Nestucca Drive, Portland, Oregon 97229.